—— How to calculate the volume of Sweet Dumpling?
Introduction
How can we optimize the materials at a dinner party for about 200 people to make the food with the largest volume?
To achieve this purpose I need to calculate the volume of the food. The food I chose is Chinese sweet dumplings and the goal of this project is to find the volume of the sweet dumpling by creating mathematical models.
Using GeoGebra as software, I modeled the sweet dumplings based on the function of inserting photographs in the geometric window as a background picture. The following essay will illustrate two methods of modeling the Chinese sweet dumplings by exploiting GeoGebra and compared the differences between the two approaches.
Data
Totally, I made 12 sweet dumplings and recorded the radius of each sweet dumplings after boiling. The average radius of 3.35cm was adopted to build the model.
| NO. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | Average |
| Diameter(cm) | 3.5 | 3.1 | 3.3 | 3.4 | 3.5 | 3.5 | 3.4 | 3.3 | 3.4 | 3.2 | 3.3 | 3.3 | 3.35 |

Method 1: Using Polynomial Models to Calculate the Volume
The Modeling Process
First of all, I inserted the picture of the sweet dumpings to GeoGebra; located one of the sweet dumpings to the origin of the coordination; and adjust the size of the picture, to make the radius of the diameter of sweet dumping to be 3.35 cm.
Secondly, with the command of the polynomial fitting, the shape of the sweet dimpling can be model by two polynomials:
y1 = -0.028x^8+0.015x^7+0.046x^6+-0.034x^5-0.028x^4+0.06x^3-0.346x^2-0.128x+1.624
y2 = 0.038x^7+0.063x^6-0.146x^5-0.056x^4+0.16x^3+0.116x^2-1.452
Then, after found the two polynomial functions, I can calculate the area between the two curves by using 𝐴 = ∫ [𝑓(𝑥) − 𝑔(𝑥)] 𝑑𝑥 (upper bond b, lower bond a). The x-coordinate of the two functions’ intersections is -1.67 and 1.674, and in the interval of [-1.67, 1.674] y1 lies above y2. In this way, I can found the area between the curves by solving 𝐴 = ∫ (𝑦1 − 𝑦2) 𝑑𝑥 = 8.17 (upper bond 1.674, lower bond -1.67, lower bond a).
Finally, by using integral of the area between the curves, I found the volume of the sweet dumpling.
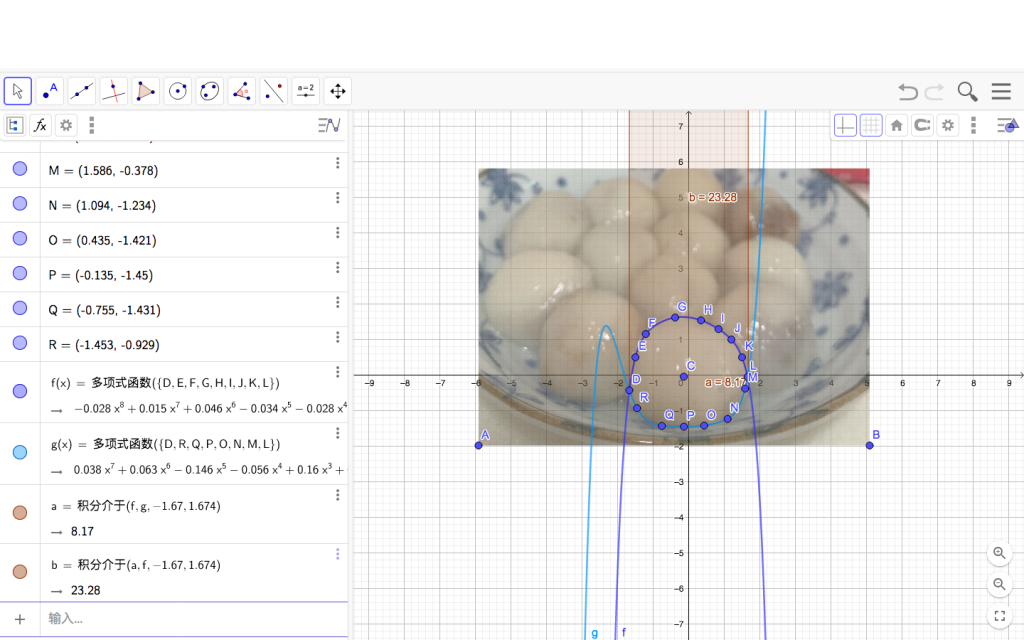
Interpreting The Model
The process of modeling is basically theory-driven. The main mathematical ideas behind this method of modeling are applying definite integral to calculate the area between curves and the volume. The volume formula is 𝑉 = ∫ 𝐴(𝑥) 𝑑𝑥 (upper bond b, lower bond a), and A(x) is the area between the two curves, which can be calculated by 𝐴 = ∫𝑏[𝑓(𝑥) − 𝑔(𝑥)] 𝑑𝑥 (upper bond b, lower bond a).
The functions that used to find the volume are listed below.
y1 = −0.028x^8 + 0.015x^7 + 0.046x^6 − 0.034x^5 − 0.028x^4 + 0.06x^3 − 0.346x^2 − 0.128x + 1.624
𝑦2 = 0.038𝑥^7 + 0.063𝑥^6 − 0.146𝑥^5 − 0.056𝑥^4 + 0.16𝑥^3 + 0.116𝑥^2 − 1.452
𝑎 = ∫ [ 𝑦1(𝑥) − 𝑦2(𝑥) ] 𝑑𝑥 = 8.17 (upper bond 1.674, lower bond -1.67)
𝑎 = ∫ [ (−0.028𝑥^8 + 0.015𝑥^7 + 0.046𝑥^6 − 0.034𝑥^5 − 0.028𝑥^4 + 0.06𝑥^3 − 0.346𝑥^2 − 0.128𝑥 + 1.624) − (0.038𝑥^7 + 0.063𝑥^6 − 0.146𝑥^5 − 0.056𝑥^4 + 0.16𝑥^3 + 0.116𝑥^2 − 1.452) ] 𝑑𝑥 = 8.17 (upper bond 1.674, lower bond -1.67)
𝑉 = 𝜋 ∫[𝐴(𝑥) − 𝑦2(𝑥)] 𝑑𝑥 = 23.28 (upper bond 1.674, lower bond -1.67)
𝑉 = 𝜋 ∫ [ (8.17 − 0.038𝑥7 + 0.063𝑥6 − 0.146𝑥5 − 0.056𝑥4 + 0.16𝑥3 + 0.116𝑥2 −1.67− 1.452) ] 𝑑𝑥 = 23.28 (upper bond 1.674, lower bond -1.67)
Method 2: Using Sphere Model to Find the Volume
The Modeling Process
First of all, I inserted the picture of the sweet dumpings to GeoGebra, and located one of the sweet dumpings to the origin of the coordination, and adjusted the size of the picture to make the diameter of the sweet dumping to be 3.35 cm, so the radius is 1.675 cm.
Secondly, with the commend of the circle through three points, I found the curve of the conic and the equation of the conic through the chosen three points, C (-0.97, 1.47 ), E (1.63, 0.15), G (-0.11, -1.71), simultaneously. The function of the circle is (𝑥 + 0.07)^2 + (𝑦 − 0.01)^2 = 2.803. Based on the function of the circle, I found the center of the circle is H (-0.07, 0.01), and its radius, 1.675 cm.
Then, to calculate the volume of the sweet dumpling the model needs to be three-dimensional. Thus, by using the commend of creating of a sphere through the sphere center H (-0.07, 0.01), and the radius 1.675 cm, I created a sphere model. The function of the sphere model is(𝑥 + 0.07)^2 + (𝑦 − 0.01)^2 + 𝑧^2 = 2.8056.
Finally, according to the sphere model, the volume of the sweet dumpling is 19.685 cm^3.

Interpreting The Model
The process of modeling is also theory-driven. The main mathematical ideas behind this method of modeling are modeling the sweet dumpling by a sphere model and using the volume formula of the sphere to calculate the volume. The volume formula of the sphere is 𝑉 = 4/3·𝜋𝑟^3. In this way, I can find the volume of the sweet dumpling simply by measured the radius.
The functions used to find the volume are listed below.
(𝑥+0.07)^2+(𝑦−0.01)^2+𝑧^2 =2.806
𝑉=4/3𝜋∙1.6753^3 =19.168 3
Comparison Of The Two Methods

Conclusion
The report illustrates two approaches to modeling the Chinese sweet dumplings in order to calculate its volume. The two approaches are using polynomial models to calculate the volume (method 1) and using sphere function to find the volume (method 2) respectively. The result of method 1 is is 𝑉 = 23.38 𝑐𝑚^3 and 𝑉 = 19.168 𝑐𝑚^3 for method 2, so the difference between the two results is 23.38 − 19.168 = 4.212 𝑐𝑚^3 , which is relatively a small difference. The main ideas behind method 1 are applying definite integral to calculate the area between curves and the volume. On the other hand, the logic of method 2 is applying the volume formula of sphere to calculate the volume.
Reference
Solids of Revolution – from the Integration of a given Function to the Modelling of a Problem with the help of CAS and GeoGebra