Reflection
At the beginning, we focus on the driving question:
“How high off the ground are we at any time?”
And the basic data was given:
- The radius of the ferris wheel is 60 meters.
- The centre of the ferris wheel is 75 meters above the ground.
- The wheel takes 30 minutes to make a single turn.
At the first stage of the explore, as a group, me and my partner choose the flavor that is driven by data. Here is the explore process:
First, we specific our goal: find the relationship between time and the height of the passenger. The two essential variables in this question are “time” and “height of the passenger”. Obviously, “time” is the independent variable and “height of the passenger” is the dependent variable in this driving question.
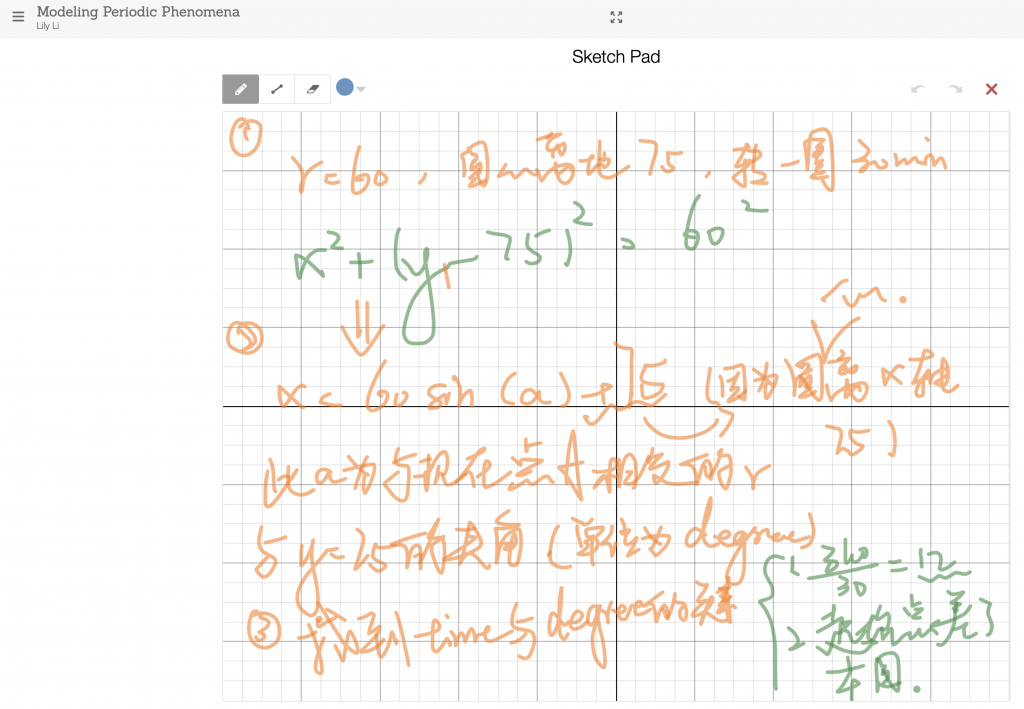
Second, we use a circle to build a model of the ferris wheel, which can represent by the function:
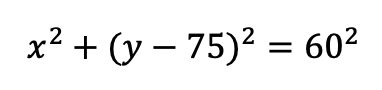
Among this function, its structure is the standard form of the circular function. So the value 75 means the y coordinate of the ferris wheel’s model, it’s come from the information that “the center of the ferris wheel is 75 meters above the ground”.
And use a line to describe the height of the passenger, which can represent by the function:
Then we can get the function:

This function is from the radius and the height of the center of the circle. But the independent variable of this function is the Angle between the radius of the current position of the cage and the line y = 75, so that we need to change the independent variable into time. Then we try to find the relationship between time and angle (measured by degree). Then we get the function for our solution:
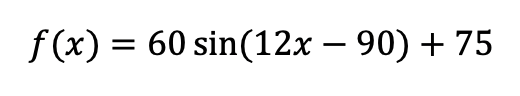
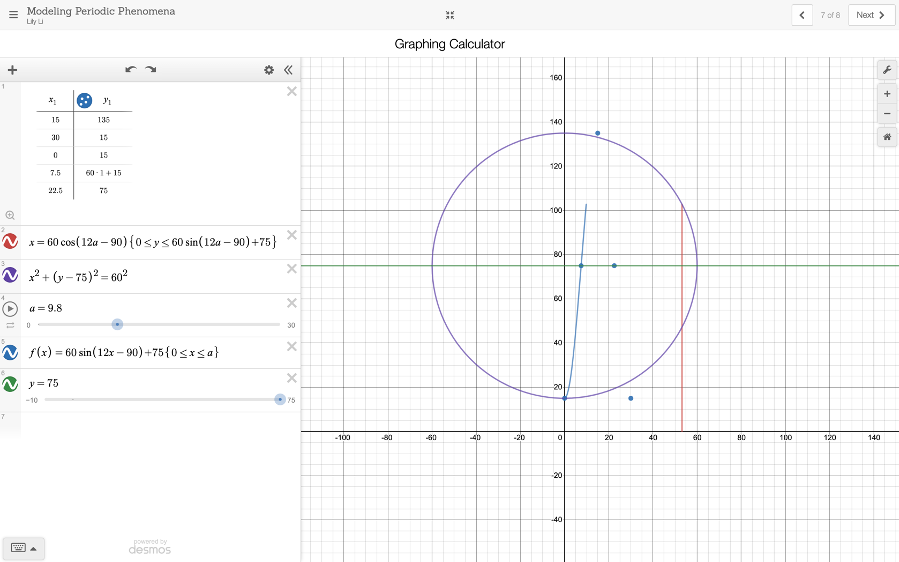
At the end, we checked the graph of the equation with the special points we calculated before and found that our function is fit to the data.
After the presentation of this exploration at class, my group receive the following questions:
- What is the value 60’s meaning in the function? Is it the radius or the amplitude?
- In the function, the input value x was minus 90, what is the meaning for doing this? Moreover, this operation on value “x” will lead to the change of coordinate value “y” at the same time, so that it requires classified discussion.
These questions let me see the “fishy” details[YD1] in our exploration process, which is that some of the values in our function is come from guessing but not thinking. Such as the “-90” in the function, it’s found by our progress of trying to move the “start state” at the bottom of the ferris wheel. And this realization also pushed an important problem in front of ourselves: We don’t really understand the meaning of the values and other elements[YD2] in our function, and that is the reason why our function looks more like a conclusion that only came from experience but not theory.
Then I try to identify possible problems in our approach by becoming familiar with the ways of others in solving the same problem.

There is a very obvious difference between our conclusion and our classmate’s conclusion: we use the degree to measure the angle, but others use radian. That makes our function more single at visual. But if we uniform unit the measure, it will be easy to find that they have the same influence on the function. So, what is the influence? I review the history that my group find this value: it influences the “beginning” of the period phenomenon.
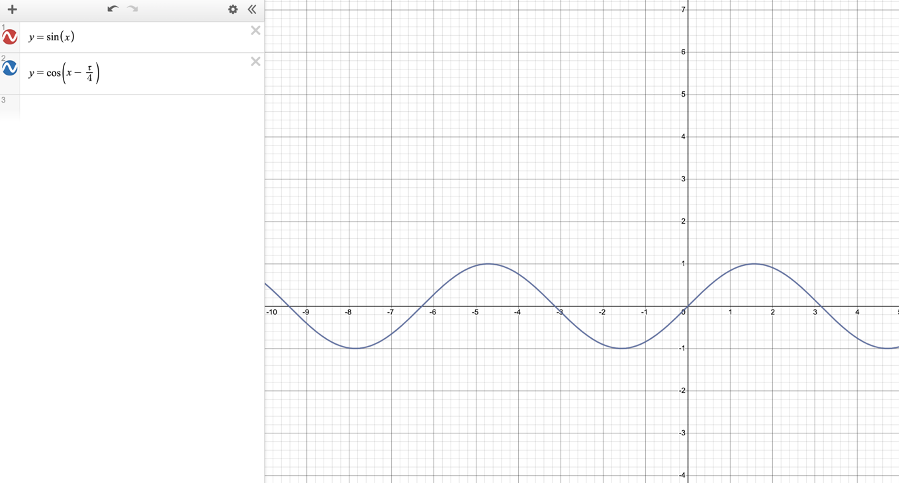
Through other classmate’s sharing, I learned that its name is “initial phase”, which can be denoted by the letter 𝛗. And at this situation, minus 90 is to set the “beginning” at the y-axis, also “ the bottom of the ferris wheel”. Here is another point about the elements in our function: the reason why the “sin” or “cos” are appearing in every function is that it can describe the period phenomenon occurs at the moving of the ferris wheel. This answered the second question we received in class. And the reason why everyone will add 75 after the consensus, is that when we build a mathematical model for the ferris wheel, we need to take into account the ferris wheel’s centre is 75 meters above the ground. But there is another problem that makes me pay attention to: we didn’t meet any problem as we try to explore the question. I think it shows that we didn’t consider the different solution of the circular function at that time. Also, the functions are divided into two categories in the table, one is sine and the other is cosine, but both categories can be used to describe the same relationship in this problem. So, we can extract the form in the third column of the table and find that y=sin(x) equals to y=cos(x-𝞃/4). It can be proved in desmos : (The graphs of two functions are overleaped).
If we look back to the definition of sine and cosine, we can find that in the unit circle, the difference between the “initial phase” of sine and cosine is tau/4. Also, the period and the amplitude or even the axis of oscillation of cosine and sine are the same. That means we can “fix” this only difference on “initial phase” by horizontally shift the graph of cosine right by tau/4 units or horizontally shift the graph of sine left by
tau/4 units.
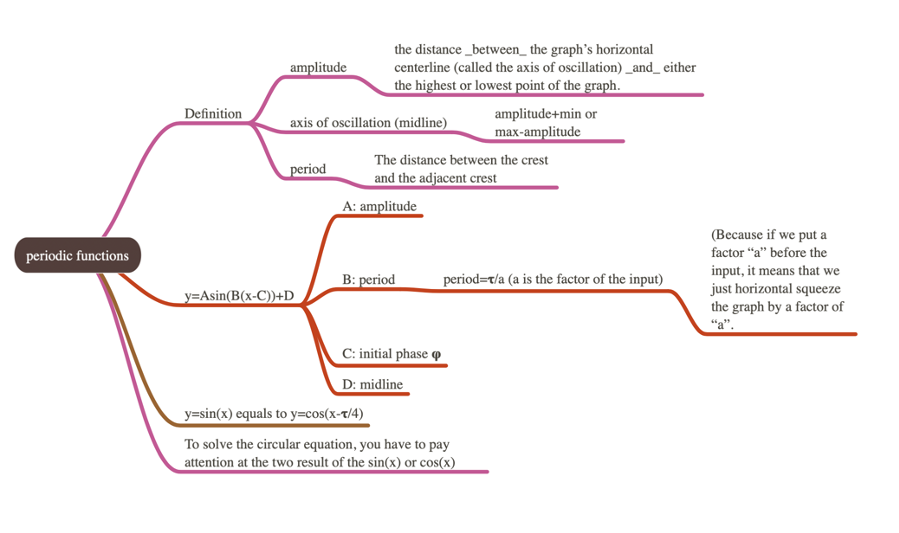
Besides, I create a mind map for the basic information of the periodic functions, it includes the definition and the operation of periodic functions that I used or learned from this exploration. Hope this can let me get familiar with the period function.
Collaboration
In the beginning, we (me and Aimee, my only partner in this exploration problem) received the assignment and specific our goal in the discussion on March 13. Obviously, this “cooperative partner” relationship is different from the traditional concept of a “team” because of that this collaboration is to support our own learning in the exploration. So the most important points we need to pay attention are the personal exploration and information balance between each other.
And the driving problem is not that complex, which let the sub-problem that we separate from the original problem is simpler than other projects. Thus, we were able to reach a consensus that one of us didn’t need to be in a traditional leadership role but need to try our best to push each other when the progress meets with setbacks. Then we clarify the independent work that we need to do after discussion. And also decided the time that we need to balance our information and help each other by our own opinion on this problem based on the experience that we work together for an exploration math problem.
The initial discussion determined that by March 14, the day after we received the task, we needed to complete the basic idea of the modelling and describe it to each other in the discussion.

As both of us have made progress, the discussion on March 14 went smoothly: in the process, she first explained her preliminary model and the problems she met. I happened to be the same with her in most solutions, and I just solved the problems she met. Then, we decided on the reporting part of the lecture on March 16: each part of the point of view that I had provided in the discussion (because it was familiar). In addition, we also remind each other to summarize the problems encountered by other groups in class and think about them.
The presentation went smoothly, and I received a more detailed feedback from Susan after the presentation, which mentioned problems we hadn’t thought about. I started thinking after I first told Aimee this information.
Since we have informed each other in advance, we attach great importance to the feedback from students and teacher during and after class. After sorting out the problems, we immediately decided to discuss again in the following two days to improve the problems we encountered.

In the last meeting, we determined the conclusion (meaning of each element in the formula) based on previous thinking and discussion on the feedback problem. Finally, I propose to comb and simplify the whole process of reaching conclusions, which I finally present on the “Sketch Pad”.